How to Read Epidemiological Parameters: Going from R0 to Predicting Number of Deaths

Basic guide for using CDC data to understand how many people must die for a society to reach herd immunity (also posted on Medium)

David J. Sencer CDC Museum in Atlanta, GA (public domain image from Jim Gathany)

An epidemic is not a single number. Knowing exactly how bad an epidemic is requires knowing both how quickly it is going to spread and how bad its effects will be on those who are affected by it. To make matters worse, parameters that characterize each of these separate factors usually cannot simply be “multiplied together” to understand their composed effects. They have to be filtered through dynamical models that properly account for depletion and saturation effects in populations. So it is understandable that the average person might have a hard time making sense of CDC estimates of such parameters, and it is not surprising that there are a lot of misconceptions and misperceptions about these topics.

Let’s take the CDC COVID-19 Pandemic Planning Scenario report (as of May 20, 2020). This looks like a simple document at first, but it may be difficult to understand how to pull all of these numbers together. For a variety of reasons, parameters of interest to epidemiologists are difficult to estimate from data. One method to mitigate issues with incomplete or noisy data is to make assumptions that help fill in the gaps, but then your analysis is only as good as your assumptions. To be conservative and to understand how sensitive predictions are to these assumptions, the CDC has come up with five different “scenarios” that stretch across a wide range of assumptions. To keep things simple, we will focus on “Scenario 5: Current Best Estimate”, which is the CDC’s best guess at where these epidemiological parameters are.

It is best to start with everyone’s favorite epidemiological parameter, R0. This is the so-called “basic reproduction number.” It is a measure of how fast a contagious infection can spread. R0 is the combination of three factors:

• The rate of interaction between an infectious (contagious) person and others in the population (referred to as “contact rate” below in some places)
• The probability that an infectious person will infect someone that they come in contact with
• How long an infectious person stays infectious (we assume that after this period, they are in a permanent recovered state where they are immune to further infection)

Essentially, R0 is a ratio of the rate that an infectious person infects others to the rate that an infectious person becomes well. This ratio can be interpreted as the number of people an infectious person infects before they themselves stop being infectious. If R0 is less than 1, then a disease will naturally die out because (on average) those infected will not be able to infect someone else before they become well. If R0 is greater than 1, then we have a so-called endemic. That means that the infectious disease will be constantly maintained at some background level; some fraction of the population will always be either currently infectious or recovered. Interestingly, this fraction is not 100%. As an infectious disease spreads through a population, the number of those who are susceptible to further infection declines to a point where it is rare for infectious individuals to encounter them (contacts with infected and recovered are far more common). This means that when susceptible individuals are rare, each infectious individual spreads less of the infection during the time window that they are infectious. This is the so-called herd immunity. A fraction of the population can stably remain susceptible because they are protected by the large numbers of others who have already had the disease and buffer them against contact with those who are currently infectious. The fraction of the population that will remain susceptible at the so-called endemic equilibrium is 1/R0. Likewise, the fraction of those in a population that must have been infected (or vaccinated, if possible) in order to achieve herd immunity is (1–1/R0). I should note that this simplified model assumes that infectious people eventually become recovered and stay that way; things get more complicated if immunity is not long lasting.

So what does the endemic equilibrium (“herd immunity”) look like for COVID-19 (assuming long-lasting immunity)? Here is what CDC estimates for R0.

CDC estimates of R0 for COVID-19

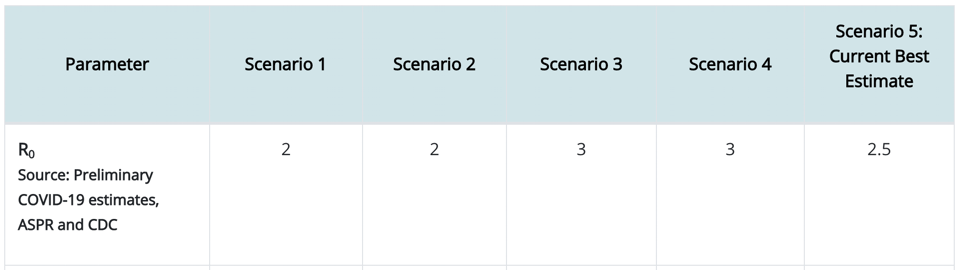
Again, focusing only on Scenario 5, we take R0=2.5, which means that any infectious person will have an opportunity to infect 2.5 other people on average. So we then estimate that 1/R0=1/2.5=40% of the population will be able to avoid infection so long as the other 60% of the population goes through an infection or is vaccinated. So exactly how many people is that? In the United States, the population is a little over 325 million people (compare this to the world population of 7.8 billion people). So that means that 60% of the 325M people in the USA must be infected to achieve herd immunity. That’s 195M people in the USA (4.68 billion people worldwide).

But not everyone who is infected sees symptoms let alone has to go to a hospital or suffers an early death. If we go back to the CDC data, we see that…

CDC estimates for asymptotic ratio and symptomatic case fatality ratio for COVID-19

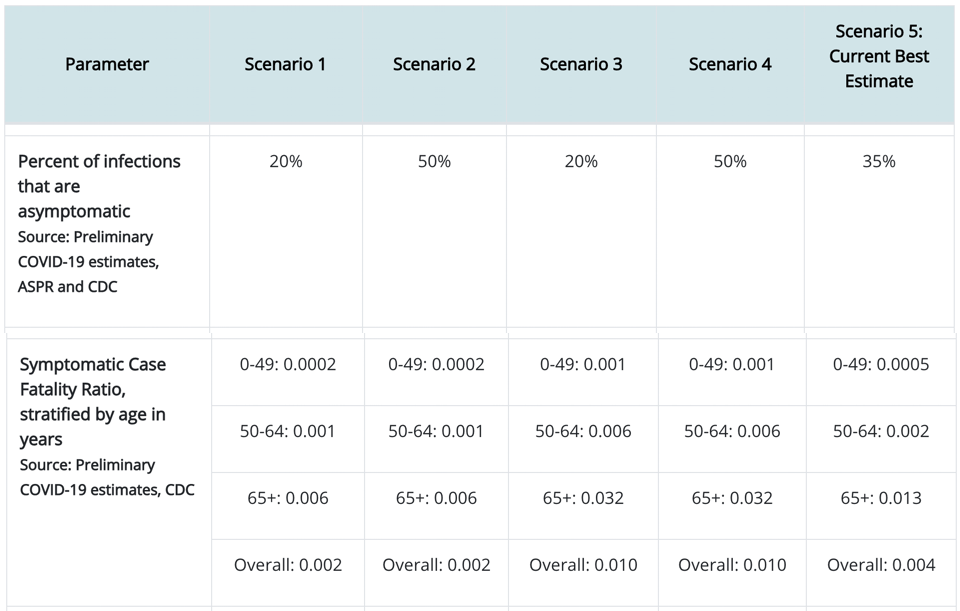
Again, looking at Scenario 5, we see that 35% of those who have an infection show no symptoms. We also see that those other 65% who show symptoms will suffer fatality at an overall (averaged across age groups) rate of 0.004 (i.e., 0.4%). That seems like a very small number! But we have to keep in mind that this is a very contagious disease (any infectious person infects 2.5 other people). So we need to combine the information on contagion with the information on case fatality rate. For the 325M people in the USA, we already calculated that 195M will have the disease. So then, at the endemic equilibrium (“herd immunity”):

• 195M*65% = 127M people will have shown symptoms in the USA
• 127M*0.4% = 508,000 people will die in the USA

And worldwide, we would expect 12.2M people will die. So even at that very small case fatality rate, there will be a lot of death (and even those that escape symptoms may still feel long-term effects of COVID-19 that we are only starting to understand now). Just as a reference, 38,000 people died in car accidents in 2018 in the USA. We try to prevent deaths by car accidents by preventing car accidents and trying to make cars safe so that people will survive accidents that happen. When we ask people to wear masks and social distance, this is not unlike people’s legal obligation to wear seatbelts and drive cars that meet safety standards.

Now, a lot of people say that there is no way to prevent these deaths, and so it is better to suffer them early instead of dragging out our march to the endemic equilibrium. In order to evaluate whether this is a good argument, we should take a look at another part of the CDC data:

CDC estimates for symptomatic case hospitalization ratio for COVID-19

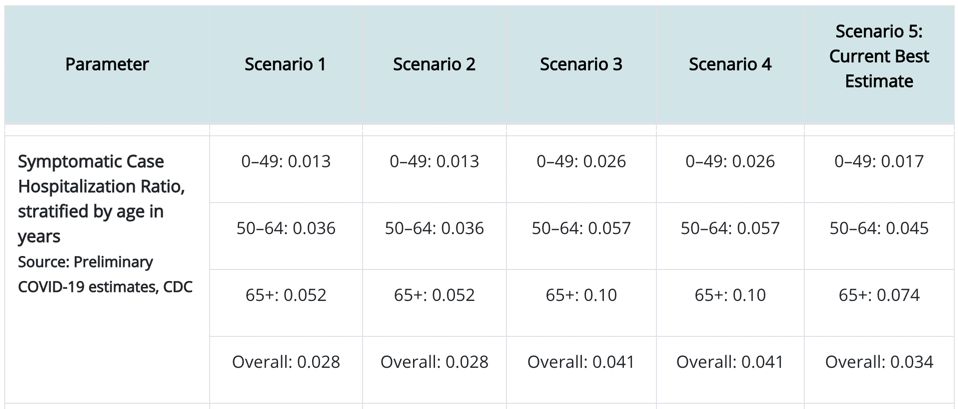
Focusing on Scenario 5’s “Overall” estimate, we see that each person who shows symptoms will have a 3.4% chance of being hospitalized. So that means we can estimate that for the population of 325M people in the USA, the 127M people we calculated above to show symptoms, 3.4% of them will have to be hospitalized, meaning that COVID-19 contribute 4.318M patients to hospitals in the USA (103M COVID-19 hospital patients worldwide). The question is whether we have enough hospital beds in the USA to accommodate these 4.318M people all at once. If we do not, then those that would have otherwise recovered will have to suffer through the disease without the support of medical professionals and medical technology. In other words, the case fatality rate for this subset of COVID-19 symptomatic individuals turned away from hospitals may rise to much higher than the 0.4% mentioned above. So this is really the essence of the movement to flatten the curve (e.g., by wearing masks and social distancing to reduce the effective contact rate). Even if it is impossible to avoid the 508,000 deaths predicted above, if infections can be spread out over a long amount of time, we can help to ensure that at any instant there will be enough hospital beds. Furthermore, if we stretch out the infection curve far enough, we may develop a vaccine within the curve’s duration. Vaccinations are a game changer because they provide a quick shortcut (that is hopefully much safer than a full-blown infection) to herd immunity.

But if we wanted to reduce that 508,000 without a vaccine, how would we do it? Remember that I said that R0 (a parameter of infection spread) is determined in part by the rate that an infectious individual contacts other individuals in the population. If we can devise long-term behavioral or technological methods to reduce this contact rate (beyond temporary inconveniences, such as wearing masks), then we can change R0 for COVID-19 for good (or at least for a sufficiently long time), thereby meaning that our endemic equilibrium (“herd immunity”) will occur with a much higher number of people who avoid infection (and even vaccination) entirely. How do we do that? Here are three potentially powerful ways.

• We can remove hand shaking and other similar kinds of contact as a greeting (thereby bringing the baseline contact rate for every individual in the population to a much lower level than it was before COVID-19).
• We can develop rapid, highly available, and frequent testing protocols that can quickly identify infected individuals so that they can be isolated (thereby bringing their personal contact rate much lower than others).
• We can develop sophisticated contact-tracing techniques that can further identify potentially infected individuals so that they can be isolated (thereby bringing their personal contact rate much lower than others).

These behavioral and technological changes can actually improve our long-term COVID-19 outcome even if a vaccine is not developed. So it may not be inevitable that hundreds of thousands of more people have to die (at the time of this writing, over 110,000 people in the USA had death certificates that indicated COVID-19 as a cause of death).

Medical professionals can develop vaccines, researchers can develop novel technologies, and we can all alter our behaviors. Unfortunately, there are additional challenges in the near future that will make all of this even more urgent. In particular, we are facing a flu season ahead of us. Individuals who contract COVID-19 and the seasonal flu simultaneously may be in an untenable situation. Additionally, the medical system will face demands not only from COVID-19 but from those with the flu (but possibly not COVID-19) who also need hospitalization. Normally the medical system would have enough capacity to serve the seasonal flu population (although there are still seasonal flu deaths every year, just not as much as COVID-19). However, if the medical system has to face flu and COVID-19 along with baseline demands and any other emergent demands (other pandemics, etc.), then that will put our society as a whole in an untenable situation. The flu shot may be especially important to encourage this season.

Of course, there are many other interesting figures in that CDC report that we could further analyze that relate to how long the average COVID-19 hospital patient takes to recover, which would help us figure out more quantitative details about the amount of each of the kinds of possible actions discussed above will be necessary to prevent hospitals reaching capacity. For now, I will leave that analysis as an exercise for the reader. In the meanwhile, get some rest, stay safe, and stay healthy!

Stochastic versus random: The difference is whether you're describing a model or a focal system

It seems like there is a lot of confusion in quantitative modeling circles over the relationship between "randomness" and "stochasticity." This is in large part because the success of stochastic models to make sense of the world around us has led to wide use of stochastic modeling, so much that "stochastic" has become a near synonym for "random." However, the two terms are not identical.

Slide from SOS 212 (Systems, Dynamics, and Sustainability), an introductory modeling course I teach

"Randomness" is a general term representing a special kind of uncertainty where the frequency of possible outcomes can be described using probabilistic methods. Where a photon is going to be at a particular instant of time is fundamentally random; it can only be described using a probability distribution. There are some kinds of uncertainty that cannot be described probabilistically. For example, I might know that an experiment can end in one of three different ways, but exactly how it will end depends upon which participant is performing the experiment. If I need to describe how the experiment can end but do not have any ability to specify a probabilistic weighting of the outcomes, I can describe the system as having a non-deterministic outcome. So something can be fundamentally random or non-deterministic. If it's random, you have some way to describe how one outcome might be more likely than another.

"Stochastic" is a term originating from Greek for "guess" or "conjecture." It describes a modeling technique to simplify a model by assuming (guessing/conjecturing) that the system being modeled is random, even if it is not. In other words, rather than having to account for a wide range of degrees of freedom that might be necessary to specify how a system is going to evolve, you substitute all of that detailed deterministic modeling with a crude approximation of the outcome being "random". The modeling burden then shifts from getting everything right down to high levels of precision to shaping the probability distributions to best match the outcomes that are most likely, regardless of what the underlying mechanism is. So a "stochastic model" is one that describes a system using randomness regardless of whether there is any reason to believe that the randomness is fundamental. It is a modeling trick to add analytically tractability to models that would otherwise be prohibitively complex to be useful.

So you shouldn't refer to phenomena themselves as being "stochastic." It is OK to say that the phenomena is random (if you really believe that). Or it is OK to say you use a stochastic model to describe the system (which implies that you will use randomness in order to omit a large number of degrees of freedom, thus making the model "simpler"). But you shouldn't use "stochastic" as a synonym for "random."

Bifurcation Diagrams, Hysteresis, and Tipping Points: Explanations Without Math

I teach a system dynamics modeling course (SOS 212: Systems, Dynamics, and Sustainability) at Arizona State University. It is a required course for our Sustainability BS students, which they ideally take in their second year after taking SOS 211, which is essentially Calculus I. The two courses together give them quantitative modeling fundamentals that they hopefully can make use of in other courses downstream and their careers in the future.

I end up having to cover a lot of content in SOS 212 that I myself learned through the lens of mathematics, but these students are learning it much earlier than I did and without many of the mathematical fundamentals. So I have to come up with explanations that do not rely on the mathematics. Here is an example from a recent lecture on bifurcation diagrams, hysteresis, and tipping points. It builds upon a fisheries example (from Morecroft's 2015 textbook) that uses a "Net regeneration" lookup table in lieu of a formal mathematical expression.

You can find additional videos related to this course at my SOS 212: System, Dynamics, and Sustainability playlist.